
Hoy quiero hablaros de una herramienta que probablemente muchos ya conocéis: MATLAB. Como estudiante de primer año de Ingeniería Informática, he descubierto MATLAB hace solo unos meses y, la verdad, me ha sorprendido gratamente. Quiero compartir con vosotros mis primeras impresiones y lo que he aprendido hasta ahora sobre esta poderosa herramienta.
¿Qué es MATLAB y para qué se usa?
Para empezar desde el principio, MATLAB es un entorno de programación y lenguaje específico utilizado para análisis de datos, visualización y cálculo numérico avanzado. Su nombre proviene de MATrix LABoratory y, como sugiere, es muy potente en la manipulación de matrices. Esto le da una gran versatilidad en áreas como:
- Ingeniería y Física: ideal para resolver problemas complejos en álgebra lineal, cálculo y simulaciones.
- Procesamiento de Imágenes: permite trabajar con imágenes y realizar análisis avanzados, útil en proyectos de visión por computadora.
- Aprendizaje Automático y Deep Learning: ofrece una variedad de herramientas para el desarrollo de modelos predictivos y análisis de datos masivos.
- Control de Sistemas y Robótica: facilita el diseño y simulación de sistemas de control, desde robots hasta sistemas electrónicos.
¿Por qué me sorprendió MATLAB?
Aunque en mi carrera el foco está más en lenguajes como C++ o Python, he descubierto que MATLAB ofrece algo único: una forma muy intuitiva de visualizar datos y de trabajar con matemáticas complejas sin complicaciones excesivas. El entorno de MATLAB permite probar y ejecutar código de manera rápida, y la visualización de resultados en gráficos es inmediata, lo cual hace que entender los datos sea muy visual y accesible.
Además, la sintaxis de MATLAB está diseñada para ser clara y precisa, algo que aprecio al venir de un enfoque más orientado a la informática clásica.
Mi Último Exámen Realizado con MATLAB
Recientemente tuve mi primer parcial de MATLAB, donde trabajé con problemas que combinaban tanto conceptos matemáticos avanzados como las herramientas de MATLAB para resolverlos de manera eficiente. Aquí os cuento un poco sobre los ejercicios que más me marcaron.
Números Complejos y MATLAB
Uno de los ejercicios consistía en encontrar las raíces de cuarto grado de un número complejo, lo cual fue una excelente oportunidad para profundizar en los números complejos y ver cómo MATLAB permite calcular y representar estos resultados en el plano complejo. Otro ejercicio nos pedía resolver y verificar la ecuación z^6 - 9z^3 + 8 = 0, un reto que MATLAB facilitó enormemente con sus funciones específicas para manejar polinomios complejos. Pude dibujar gráficos representativos de estos resultados, lo que realmente ayuda a visualizar soluciones en este tipo de problemas.
Límites y MATLAB
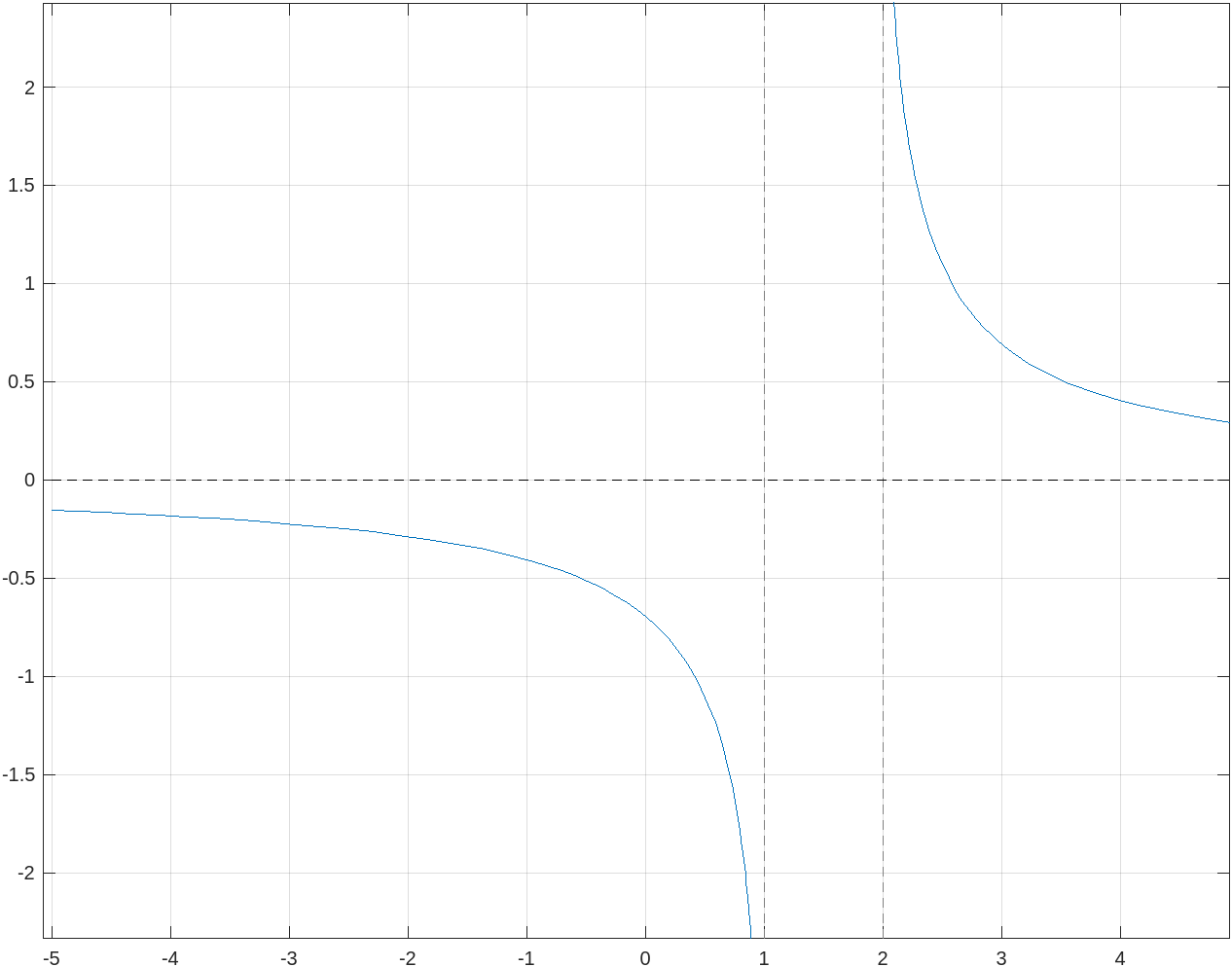
Otro bloque del exámen fue sobre límites y continuidad. En el primer ejercicio, trabajamos con una función compuesta y tuvimos que analizar su discontinuidad en un punto específico, además de representar gráficamente el comportamiento de la función. El segundo ejercicio fue aún más interesante, pues nos pedía hallar asíntotas y el dominio de una función definida como:
-ln((x-2) / (x+1))
Gracias a las capacidades gráficas de MATLAB, visualizar las asíntotas y el dominio fue sencillo y claro.
Sensaciones del parcial de MATLAB
En general, el parcial salió bastante bien. Creo que conocer la teoría matemática me ayudó mucho a adaptarme a MATLAB rápidamente, ya que los comandos básicos son sencillos y el entorno es intuitivo. Aquí os dejo algunos de los comandos que utilicé en MATLAB:
%% COMANDOS DE MATLAB
% 1. Operaciones Matemáticas Básicas
% Suma: +
% Resta: -
% Multiplicación: *
% División: /
% Potencia: ^
% Módulo (residuo): mod(x, y)
% 2. Constantes
% Número Pi: pi
% Número e: exp(1)
% 3. Funciones Trigonométricas
% Seno: sin(x)
% Coseno: cos(x)
% Tangente: tan(x)
% Arcoseno: asin(x)
% Arcocoseno: acos(x)
% Arcotangente: atan(x)
% 4. Funciones Hiperbólicas
% Seno hiperbólico: sinh(x)
% Coseno hiperbólico: cosh(x)
% Tangente hiperbólica: tanh(x)
% 5. Funciones Exponenciales y Logarítmicas
% Exponencial: exp(x) (es decir, e^x)
% Logaritmo natural: log(x)
% Logaritmo base 10: log10(x)
% Raíz cuadrada: sqrt(x)
% 6. Funciones Matemáticas Especiales
% Valor absoluto: abs(x)
% Redondeo: round(x) (redondea al entero más cercano)
% Redondeo hacia abajo: floor(x)
% Redondeo hacia arriba: ceil(x)
% Factorial: factorial(x) (solo para enteros no negativos)
% Máximo de un vector o matriz: max(x)
% Mínimo de un vector o matriz: min(x)
% Media de un vector o matriz: mean(x)
% Suma de elementos de un vector o matriz: sum(x)
% 7. Funciones Complejas
% Parte real de un número complejo: real(x)
% Parte imaginaria de un número complejo: imag(x)
% Módulo de un número complejo: abs(x)
% Argumento de un número complejo: angle(x)
% Conjugado de un número complejo: conj(x)
% 8. Funciones de Matrices
% Transpuesta de una matriz: transpose(A) o A'
% Inversa de una matriz: inv(A)
% Determinante de una matriz: det(A)
% Producto de matrices: A * B
% Elemento en una posición específica: A(i, j)
% 9. Pintar Funciones y Otros
% Pintar una funcion: fplot(Funcion, [-5 5])
% Pintar Punto Bordes: plot(x, y, 'ro', 'MarkerSize', 10)
% Pintar Punto Relleno: plot(x, y, 'ro', 'MarkerSize', 8, 'MarkerFaceColor', 'r')
% Activar cuadricula: grid on
% Seguir pintando: hold on
% Terminar de pintar: hold off
% Axis de la grafica: axis([-x x -y y])


